R markdown 사용법
환경 : windows 7 32bit, R 3.1.1 Rstudio
참고 : http://rmarkdown.rstudio.com/authoring_basics.html
1. 항목 들여쓰기 사용법
; 들여쓰는 줄에서 앞에 space 4개 넣고, + 기호 입력후 내용 적어 넣는다.
예)
- kde2d(x,y,n)
+ x,y - 변수명
+ n - 각 축의 그리드 점의 수
2. 그림 삽입하기
형식 :

예 :

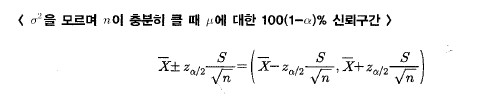

-- 로컬 image 는 full path 지정해야함.
-- github 에 올린 그림은, github 해당 그림파일 선택하면 이미지 보이면 , right click 하여 '이미지 url 복사' 선택하여, 복사한 url 을 사용하라.
3. 현재 working directory 알아내기 및 설정하기.
참고 : https://stat.ethz.ch/R-manual/R-devel/library/base/html/getwd.html
getwd()
setwd(dir)
4 . 들여쓰기
참고 : https://daringfireball.net/projects/markdown/syntax#blockquote
-- BLOCKQUOTES 사용한다.
> ==> 한번 들여쓰기
>> ==> 2번 들여쓰기
5. 수식 입력하기
참고 : http://www.calvin.edu/~rpruim/courses/m343/F12/RStudio/LatexExamples.html
http://www.statpower.net/Content/310/R%20Stuff/SampleMarkdown.html
http://rstudio-pubs-static.s3.amazonaws.com/18858_0c289c260a574ea08c0f10b944abc883.html
http://en.wikibooks.org/wiki/LaTeX/Mathematics
$A \cap B$
$A \cap B$
$A \cup B$
$A \cup B$
$x \in A$
$x \in A$
$5 \pm 2$
$5 \pm 2$
$\log(x)$
$\log(x)$
$\sin(x)$
$\sin(x)$
$\sqrt{27}$
$\sqrt{27}$
$\overline{x}$
$\overline{x}$
$\frac{k}{n}$
$\frac{k}{n}$
$\binom{k}{n}$
$\frac{\partial f}{\partial x}$
$x^2$
$x_2$
$\lim_{x\to\infty}$
$\displaystyle \lim_{x\to - \infty}$
$\int_0^{\infty} f(x) \; dx$
$\displaystyle \int_0^{\infty} f(x) \; dx$
$\alpha A$
$\beta B$
$\gamma \Gamma$
$\delta \Delta$
$\epsilon E$
$\varepsilon E$
$\zeta Z$
$\eta \Eta$
$\theta \Theta$
$\iota I$
$\kappa K$
$\lambda \Lambda$
$\mu M$
$\nu N$
$\xi \Xi$
$\omicron O$
$\pi \Pi$
$\rho P$
$\sigma \Sigma$
$\tau \Tau$
$\upsilon Y$
$\phi \Phi$
$\varphi$
$\chi X$
$\psi \Psi$
$\omega \Omega$
$x \ge 15$
$a_i \ge 0~~~\forall$
$$\int_0^{2\pi} \sin x~dx$$
$$\begin{array}
{rrr}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}
$$
$$\mathbf{X} = \left[\begin{array}
{rrr}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}\right]
$$
$\alpha, \beta, \ldots$
$\dots$
$\times$
$3 \div 5$
$\prod_{n=1}^N$
$<, \leq, \geq$
$\sim$
$\widehat{\alpha}$
$\bar{x}$
$\left(\frac{a}{b}\right)$
$y_i = \alpha + \beta x_i + e_i$
$\frac{1}{1+\exp(-x)}$
$$\frac{1}{1+\exp(-x)}$$
$\frac{1}{n} \sum_{i=i}^{n} x_{i}$
$\begin{aligned}
\dot{x} & = \sigma(y-x) \\
\dot{y} = \rho x - y -xz \\
\dot{z} = -\beta z+xy
\end{aligned}$
$\overline{X} \pm z_{\alpha/2} \frac{S}{\sqrt n} = ( \overline{X} - z_{\alpha/2} \frac{S}{\sqrt n} , \overline{X} + z_{\alpha/2} \frac{S}{\sqrt n} )$
$t = \frac{\overline{X} - \mu}{S/\sqrt n}$
$\overline{X} \pm t_{q,\alpha/2} \frac{S}{\sqrt n} = ( \overline{X} - t_{q,\alpha/2} \frac{S}{\sqrt n} , \overline{X} + t_{q,\alpha/2} \frac{S}{\sqrt n} )$
$(\frac{qS^2}{\chi_{(q,\alpha/2}^2)} ,
\frac{qS^2}{\chi_{(q,1-\alpha/2}^2)} )$
$\displaystyle SSB = \sum_{j=i}^J n_j (\overline X_j - \overline X)^2$
$\displaystyle SSE = SS_1 + SS_2 + \dots + SS_j = \sum_{j=1}^J\sum_{i=1}^{n_j} (x_{ij} - \overline X_j)^2$
$\chi^2 = \sum \frac{(O-E)^2}{E}$
$E_{ij} = \frac{RT_i \times CT_i}{n}$
'기타' 카테고리의 다른 글
| tistory 에서 mathjax 사용하기 (0) | 2015.01.05 |
|---|---|
| windows 에서 elasticsearch 설치하기 (0) | 2015.01.02 |
| git 설치 및 사용하기 (0) | 2014.12.12 |
| R markdown Slidy 에 rCharts 결과 그래프 넣기 (0) | 2014.10.27 |
| R -- rCharts 설치 실행하기 (0) | 2014.10.25 |



